Кружок 1С #2. Двоичный поиск (бинарный, дихотомия) в 1С

Условие задачи

Нужна возможность осуществлять анализ введенного пароля на то, что он скомпрометирован путем анализа файлов часто используемых паролей.

Итого: у нас есть введенный пользователем пароль, и нам необходимо путем перебора нескольких макетов с часто используемыми паролями, в которых на каждой строке введен пароль в нижнем регистре определить совпадает ли введенный пароль с тем, который ввел пользователь с теми паролями, которые есть в файле. Если он найден, надо написать, что пароль скомпрометирован. Обращаю внимание, что мы опускаем то, что регистр может быть другим. Будем введенную строку пользователя переводить в нижний регистр и проверять только маленькие буквы. Это упрощает задачу.

Первый вариант решения "в лоб"

В самом начале, я попытался использовать поиск "в лоб". Т.е. берем по очереди макеты с паролями и строчка, за строчкой сравниваем с тем, что ввел пользователь. Нашли - отлично, пароль скомпрометирован, если не нашли, то так и напишем.

Проблема оказалось в том, что для ~88000 часто используемых паролей это работает ОЧЕНЬ медленно. На моем компьютере это отрабатывало около 18 секунд. Пользователь не захочет ждать такое время. Значит нам нужен другой алгоритм.

Второй вариант решения: двоичный (бинарный) поиск или дихотомия

Дальше, я начал думать, как же можно было бы улучшить алгоритм. И вспомнил про двоичный поиск. Начнем с определения из вики.

Двоичный (бинарный) поиск (также известен как метод деления пополам или дихотомия) — классический алгоритм поиска элемента в отсортированном массиве (векторе), использующий дробление массива на половины. Используется в информатике, вычислительной математике и математическом программировании.

Важно, что все слова наших паролей упорядочены по алфавиту. Схематично алгоритм выглядит так:

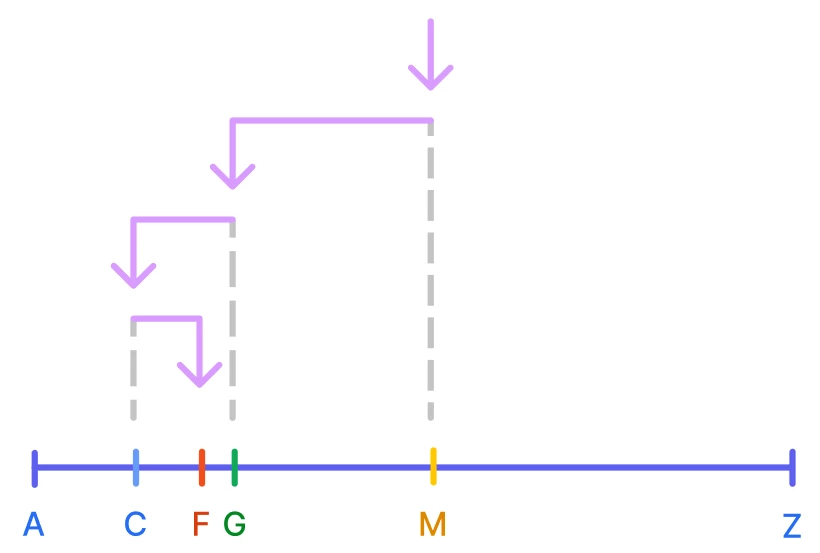
Предположим наше слово начинается на букву F.

1. В самом начале левой точкой мы берем букву A, правой букву Z. Центральная точка у нас M.
2. M нужная нам точка? Если бы это была искомая буква, то мы ее нашли и должны закончить, но нет, это не наша точка, продолжаем алгоритм.
3. В каком отрезке может находится нужная нам точка F в AM или MZ?
4. Наша искомая точка находится в AM, тогда в качестве левой точки выбираем А, в качестве правой, выбираем M и продолжаем, переходя на шаг 1.

Вариантов окончания работы алгоритма всего два: либо мы наткнемся на эту точку на очередном шаге и нужный элемент найден, либо у нас не останется больше точек и это будет означать, что мы ничего не нашли и элемент не найден.

Реализация алгоритма двоичного поиска на 1С

// Проверить присутствие пароля в списке скомпрометированных паролей.
// 
// Параметры:
//	Макеты - Массив - Массив, каждый элемент которого является текстовый файл со строками
//  Пароль - Строка - Пароль
// 
// Возвращаемое значение:
//  Булево - Присутствие в списке доступных паролей.
Функция ПарольСкомпрометированДихотомия(Макеты, Пароль) Экспорт
	
	Если ПустаяСтрока(Пароль) Тогда
		Возврат Ложь;
	КонецЕсли;
	
	нПароль = СокрЛП(НРег(Пароль));
	ПоловинаОтрезка = 2;
	Шагов = 0;

	// Проверка того, что пароль в нижнем регистре встречается в базах часто используемых паролей.	
	Для Каждого ТекстМакета Из Макеты Цикл
		
		// Поиск методом "Дихотомии".			
		Лево = 1;
		Право = СтрЧислоСтрок(ТекстМакета);		
		Пока Лево <= Право Цикл
			
			Центр = Лево + Цел((Право - Лево) / ПоловинаОтрезка);
			Стр = СтрПолучитьСтроку(ТекстМакета, Центр);				
			Если нПароль < Стр Тогда
				Право = Центр - 1;
			ИначеЕсли нПароль > Стр Тогда
				Лево = Центр + 1;
			Иначе
				Возврат Истина;
			КонецЕсли;
			Шагов = Шагов + 1;
			
		КонецЦикла;
		
	КонецЦикла;
	
	Возврат Ложь;
	
КонецФункции

Используйте алгоритмы друзья! В заключении приведу ссылку с видео-демонстрацией с нашего канала.

Видео с нашего канала Кружок 1С #2